Quote:
Originariamente inviata da GIGID
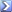
Se faccio una curva ai 50 con 20 gradi … ai 100 sono a 40 ?
|
Azz che domandone !!


Non è così lineare, ma un po’ più arzigogolato …sicuro sicuro che lo vuoi sapere??

Partiamo dalla fisica:
un corpo durante un moto curvilineo è sottoposto ad una accelerazione centrifuga che è il rapporto tra il quadrato della velocità e il raggio di curva : Ac= V^2 / r
La forza centrifuga che ne deriva è il prodotto di tale accelerazione per la massa, si applica al baricentro dell’insieme moto-pilota ed è rappresentata dalla freccia rossa nella foto qui sotto.
Dalla formula si scopre che aumenta col quadrato della velocità , quindi se la velocità raddoppia la forza quadruplica!

Essa tende a spingerci all’esterno…
La moto sta in equilibrio ad una determinata inclinazione quando l’angolo di piega è tale per cui il vettore risultante tra l’accelerazione di gravità “g” e la forza centrifuga “V^2/r passa esattamente sulla linea che congiunge i punti di contatto a terra delle due ruote
Questa risultante è la freccia verde, e la sua componente al suolo è quella blu che ho disegnato io, che devi immaginare applicata anch’essa al baricentro, e tende a farci cadere all’interno. Chiamiamola “H”, ma si chiama “reazione centripeta”.
La rossa tira da una parte, la blu dall’altra… se sono uguali la moto sta in equilibrio.
Come facciamo a trovare l’angolo che mette le due forze in equilibrio?
Ci tocca tirare in ballo la trigonometria, ed esattamente il 3º teorema sui triangoli rettangoli: “in un triangolo rettangolo la misura di un cateto è data dal prodotto tra la misura dell'altro cateto per la tangente dell'angolo opposto al primo”
Nella nostra figura, la linea gialla (g , l’accelerazione di gravità ) e quella blu (V^2 / r , la reazione centripeta) formano un triangolo rettangolo di cui rappresentano i due cateti, la linea verde è l’ipotenusa che forma con la linea gialla l’angolo che dobbiamo determinare (cioè l’angolo di piega) che chiamiamo per comodità P (Piega)
In soldoni: la forza centrifuga è la forza di gravità moltiplicata per la tangente dell’angolo di piega! E questo ci tornerà utile dopo…
Applicando il teorema :
V^2/r = g * tan P
Ossia tan P = V^2 / (g*r)
Da cui risulta che l’angolo P è l’angolo (o arco) la cui tangente è il rapporto tra il quadrato della velocità e il prodotto tra l’accelerazione di gravità e il raggio di curva, cioè:
P= arctg [V^2/ (g*r) ]
Tornando al tuo esempio: se in una curva con un determinato raggio sei in piega a 20° hai una forza centrifuga che è g* tan20, cioè 0,364g , circa il 36.4% di 1g, indipendentemente dalla velocità (ma poniamo pure che sia 50km/h come hai detto tu) .
Raddoppiamo la velocità a 100 km/h (27,78 m/s) : la forza centrifuga diventa 1,458 g, e per contrastarla dovresti piegare a 55,5° !
Da tutta questa zuppa estenuante (scusatemi… ma la colpa è di Gigid!!!


) scaturisce uno spunto di riflessione.
Abbiamo visto che la forza centrifuga che ci spinge in fuori è sempre uguale al nostro peso moltiplicato per la tangente dell’inclinazione in piega…questa è la forza a cui le nostre gomme si oppongono per non perdere aderenza: calcoliamola a varie inclinazioni:
39° … 0.81 g
42° … 0.9 g
45° … 1 g esatto, è il punto di pareggio tra il peso che agisce in verticale sulle gomme e la forza che spinge la moto all’esterno. Da qui in avanti il rapporto tra “ciò che ci vuole spingere nel fosso” e “ciò che ci tiene attaccati alla strada” si sbilancerà sempre di più a favore del … fosso!
47° … 1.07 g
49° … 1.15 g
51° … 1.235 g
53° … 1.327 g
Come si nota, aumenta proporzionalmente di più di quanto aumenti l’inclinazione.
Tapatalk



